Az ember már a kezdetektől fogva használt a számláláshoz segédeszközöket. Kezdetben az ujjait, utóbb különböző eszközöket: köveket, fadarabokat, pálcákba vésett rovásokat, zsinegre kötött csomókat.
A számolólécek megkönnyítették a tíznél nagyobb számok összeadását és kivonását. A számolópad (számolódeszka) sorokra és oszlopokra beosztott felületén “állította ki a számlát” az eladó a vevőnek. Útjaikra a kereskedők számolódeszka helyett ugyanígy működő számolókendőt vittek magukkal.
A számolás, a négy alapművelet megkönnyítésére már az ókorban készítettek egyszerű számolóeszközt, az abakusz-t. Az abakusz szó semita eredetű, táblácskát jelent.
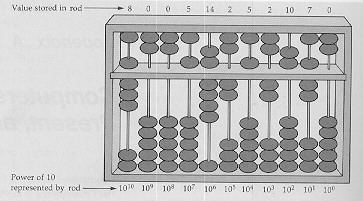 |
(Az abakusz legegyszerűbb változatában minden rúdon tíz golyó található. A golyóknak olyan elrendezése, amelyben az egy rúdon lévő valamennyi golyó szorosan a jobb oldalon helyezkedik el, az illető rúd által jelentett helyi értéken 0 számjegyet jelöl. Ha valamelyik rúdon n golyót bal oldali ütközésig elhúzunk, akkor ez az elrendezés a rúd által jelentett helyi értéken n számjegyet jelöl. |
Ha valamelyik rúdon n golyót bal oldali ütközésig elhúzunk, akkor ez az elrendezés a rúd által jelentett helyi értéken n számjegyet jelöl. Egy hatsoros (hat rudat tartalmazó) abakuszon tehát a legnagyobb ábrázolható szám 999999.
Ha az abakusz elválasztó lécet tartalmaz, akkor minden rúd elválasztó léc alatti részén öt (egyeseket jelölő), a felső részén pedig kettő (ötösöket jelölő) golyó elegendő a számok ábrázolásához. (képen)
Ennél is kevesebb golyót tartalmaz a (4+1)-es abakusz, amely azt használja ki, hogy minden számjegy ábrázolásához csak 1 ötösöket és 4 egyeseket jelölő golyóra van szükség, a kerethez ütköző golyó pedig mindig nulla helyzetet jelent. Az összeadás és kivonás az abakusszal egyszerűen és gyorsan elvégezhető. A szorzás és osztás több gyakorlatot és időt igényel.)
Már az abakusznál megjelenik a számítástechnika három alapfogalma: a helyi érték, az átvitel, az eltolás.
A római kultúra átvette az abakusz használatát, saját számítási rendszeréhez igazította. Ezek a római számírásnak megfelelő, egy-egy önálló jellel rendelkező számot jelentettek.(1 I , 5 V , 10 X , 50 L , 100 C , 500 D , 1000 M). A római számok esetében nincsenek helyi értékek – az un. additív számrendszerek közé tartozik – , itt az egyes jegyek értékét a megfelelő szabály szerint a jegyek összeadásával, kivonásával képezzük.
Az abakusz évszázadokig egyeduralkodó számítási segédeszköznek bizonyult. Széles körű elterjedéséhez hozzájárult, hogy elsajátításához nem volt szükség az írásbeliség ismeretére.
A Püthagorasz-féle számolódeszka az ókori Görögországban kifejlesztett számolási segédeszköz. A gyakran szükséges számításokat egy-egy táblázatban foglalták össze, amelyből az eredményeket egyszerűen leolvasták. A Püthagorasz-féle számolódeszka a matematikai táblázatok ősének tekinthető. Például:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
|
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
|
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
|
|
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
6 X 7 = 42 |
|
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
|
|
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
Az indiai eredetű tízes alapú helyi értékrendszer elterjedése tette olyan egyszerűvé a számításokat, hogy versenyre kelhetett az abakusszal.
Már a II. századtól kezdve az indiai számrendszerben különböző jele volt az első 9 természetes számnak. A naptári adatok helyi értékes írásmódja már a VI. század óta ismert Indiában, de még a nulla használata nélkül. A helyi értékrendszerhez szükség volt még egy, a nullát kifejező számjegyre. A nulla azt fejezi ki, hogy a megfelelő helyen nem szerepel tíz megfelelő hatványa. A tízes számrendszer a VII. századra alakult ki teljesen.
Európában a fennmaradt legrégibb kézirat, amely már a tízes számrendszert és az új számjegyeket használta a 976-ban az észak Hispániai Logorno város közelében lévő Albedo kolostorban készült Codex Vigilanus.
Az első nyugati tudósok egyike, aki az arab matematikát tanulmányozta Gerbert francia szerzetes volt, aki 999 és 1003 között II. Szilveszter néven pápa volt. Ő küldte Szent István királyunk koronáját.
Európában a tízes számrendszer használata nehezen tört utat magának. A számítások hagyományos, megszokott formáiban csak a XII. század vége felé következett be lényeges változás. Az igazi áttörést 1202 jelentette, amikor megjelent Leonardo Pisano műve: Az abakusz könyve. (Itt az abakusz kifejezést az aritmetika, azaz számolástan szinonimájaként értelmezzük, mert Itáliában még később is ilyen értelemben használták.) Leonardo Pisano 1170 körül született Pisában és 1240 után halt meg. Apját ragadványnevén Bonaccionak, azaz jólelkűnek nevezték, ezért a könyvön szerzőként Fibonacci, tehát Bonaccio fia szerepelt. Fibonacci ebben a könyvben az arabok munkáiból merített hatalmas ismeretanyagot rendszerezte, illetve kiegészítette a görög matematikai ismeretekkel, valamint hozzátette saját matematikai módszereit és feladatait. A X. századtól kezdve még bő fél évezrednek kellett eltelni, hogy a tízes számrendszer és az új számjegyek használata a mindennapi életben is elterjedjen.
A gelosia-módszer (rácsos módszer) a középkor kezdete óta széles körben elterjedt. Először Indiában, Perzsiában, Kínában és az arab kultúrkörben jelent meg. Európában a 14. század elején vált ismertté. (A név a korai olasz építészet geometrikus, osztott rácsos ablakkereteinek nevéből származik.)
Függőleges és vízszintes vonalak egy mátrixot képeznek. Minden mezőt egy átló két részre oszt. A szorzáshoz a szorzandó számjegyeit oszlopról oszlopra haladva a legfelső sorba, a szorzó számjegyeit pedig a legkülső oszlop egymás alatti soraiba írjuk. A felhasználó a mátrix minden egyes mezejét a hozzátartozó oszlop és sor szorzatát jelentő két számmal tölti ki. Az egyeseket az alsó, a tízeseket a felső háromszögbe írja. A teljes szorzatot úgy kapja meg, hogy a jobb alsó saroktól kezdve a bal felső sarok felé haladva összeadja a felrajzolt, egymással szomszédos átlókon elhelyezkedő számokat. Ha valamelyik átlós összeg kétjegyű szám, annak első jegyét a felette álló átlós összeghez adja. Ilyen módon jobbról balra haladva számjegyenként megkapja a végeredményt.
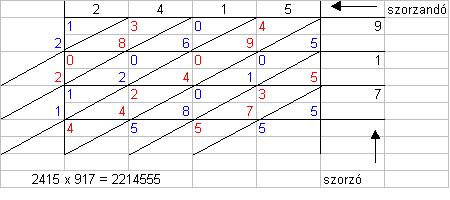
Gelosia-féle szorzás
John Napier (latinosan Neper) számolópálcákkal egyszerűsítette a rácsos módszert. A pálcákat Neper-pálcáknak vagy Neper-csontoknak is nevezték, mivel a tartósabb darabok készítéséhez Napier csontot használt. Minden pálca a rácsos (gelosia-) mátrix egy lehetséges oszlopát, tehát egy számjegy egész számú többszöröseit ábrázolta.
Meg kell említenünk még egy XV. századi iráni asztronómus és matematikus nevét, Dzsámsid ben Masszud ben Mahmud Gijjád ed Din al Kashi (1393 – 1449), és az általa készített különleges műszerekről néhány szót szólni. A szamarkandi csillagászati obszervatórium vezetője volt.
 |
(Ulug Beg, Timurlenk unokája nevéhez fűződik a háromszintes csillagvizsgáló építése Szamarkandban.) A képen a hatalmas kettős ív látható, amelyet a Nap, a Hold és a bolygók megfigyelésére használtak; sugara 40 m volt, s fokbeosztással ellátott bronzpálya tartozott hozzá. Precíz csillagászati táblázatok készültek itt 1437-ben, az év pontos időtartamát is kiszámították. |
Al Kashi használt elsőként tizedestörtet, kiszámította 2p értékét tizenhat tizedesjegy pontossággal. Konjunkciós lemeze olyan eszköz volt, amellyel meg lehetett állapítani, mikor van két bolygó konjunkcióban, azaz ugyanazon hosszúsági fok mentén. Holdfogyatkozást számító gépe zseniális eszköz volt. Planetáris számológépével a Nap, a Hold és a látható bolygók földrajzi hosszúságát lehetett megállapítani.
Az 1600-as éveket vízválasztónak tekinthetjük a tudománytörténetben. Galilei (1564-1642) előtt is léteztek természetesen szellemi óriások, azonban ő tette meg azt a hatalmas lépést, amit a természettudományok matematizálásának nevezünk.
A navigáció, a csillagászat, a kereskedelem egyre hosszabb és fárasztóbb számításokat követeltek.
1580 körül Francois Vieta (1540-1603) bevezette a matematikába a betűk használatát az ismeretlenek és az általános paraméterek jelölésére.
 |
A 16. század vége felé az egyik legjelentősebb tudományos teljesítmény a logaritmus feltalálása volt. Jost Bürgi (1552-1632) 1588-ban, 1594-ben pedig John Napier (képen;1550-1617), a skóciai Merchiston földesura, egymástól függetlenül, feltalálták a logaritmust. Edmund Gunter (1581-1626) 1620-ben elkészítette a logarléc ősét, majd 1632-ben William Oughtred (1575-1660) és tőle függetlenül Richard Delamine is készített logarlécet. Mai napig használatos alakja Partridge-től származik (1650).
Megindult a táblázatok készítése és közreadása. Logarléccel a szorzás, osztás, hatványozás, gyökvonás, logaritmus és trigonometrikus függvényértékek kiszámítása végezhető.
|
A nagy tömegű számítási művelet elvégzése miatt a matematikusok és a fizikusok maguk próbáltak számológépet szerkeszteni.
A technikatörténetben számológépnek az az eszköz tekinthető, amely műveletvégzés közben a helyi értékek közötti átvitelt külön emberi beavatkozás nélkül végzi el
 |
Történetünk a harmincéves háború idején, Wilhelm Schickard-dal (1592-1635) kezdődik, aki Tübingenben a csillagászat, a matematika és a héber nyelv professzora volt. 1957-ben dr. Franz Hammer, a Kepler irattár segédgondnoka felfedezett néhány levelet, amelyet Schickard írt Keplernek. Ezek a levelek vázlatokat és leírásokat tartalmaztak egy, a Schickard által 1623-ban tervezett és épített gépről, amely az összeadás és a kivonás műveletét teljesen, a szorzást és osztást pedig részben automatizálta. Az első levél 1623. szeptember 20-án kelt, a második 1624. február 25-én. Az elsőben Schickard azt írja a gépről, hogy “az adott számokkal automatikusan számol: összead, kivon, szoroz és oszt. Bizonyára örülne, ha látná, hogyan gyűjti össze [a gép] a tízes és százas maradékokat, vagy kivonáskor hogyan vesz el belőlük…” |
1624-es levelében így ír: “Megrendeltem az Ön számára a gép egy példányát egy helybeli mesterembernél, Johann Pfisternél; amikor azonban a gép már félig kész volt, néhány más holmimmal, főleg fémtálakkal együtt áldozatul esett az elmúlt éjszaka váratlanul kitört tűznek… Súlyosan érint a veszteség most, mivel a műszerésznek nincs rá ideje, hogy hamarosan pótolja.”
Schickard 1623-ban a négy alapművelet elvégzésére alkalmas mechanikus számológépet épített, amely az összeadást, kivonást teljesen, a szorzást és az osztást pedig részben automatikusan végezte.
A gépnek egyetlen példánya sem maradt fenn, de báró Bruno von Freytag-Löringhoff professzornak Erwin Epple műszerészmester és mások segítségével sikerült a készüléket a levélbeli információk alapján rekonstruálni, és építettek néhány működő modellt.
(A számológép felső része függőlegesen elrendezett, hengeres Neper-pálcákat tartalmaz. Forgatható gombokkal ezeken legfeljebb hatjegyű számokat lehet beállítani. Alatta fogaskerekekből készített számlálómű található. A felhasználó a Neper-pálcákról leolvasott részeredményeket kézzel viszi át a számlálóműbe. A végeredmény a készülék alján levő kis nyílásokban jelenik meg. A gép alapzatában elhelyezett számlapok hatjegyű számok tárolását teszik lehetővé, valószínűleg azért, hogy a felhasználónak a részeredményeket ne kelljen külön leírnia.
Az összeadást végző számlálóműben a szomszédos számjegyek fogaskerekei közé elhelyezett járulékos fogaskerék végzi a kétjegyű összeg első jegyének átvitelét a következő helyi értékre. A számjegyek fogaskerekeinek minden teljes körbefordítása után egy külön beépített, egyedi fog a megfelelő járulékos fogaskereket 36 fokkal elfordítja, ami viszont a következő számjegy fogaskerekét az eggyel magasabb számértéknek megfelelő helyzetbe fordítja tovább.
Schickard hat jegyre korlátozta számológépét. 999999+1 összeadásakor az egyes számjegyhez kapcsolódó egyetlen fogaskerékfognak kellene a teljes számolóművet mechanikus úton átfordítania. Ez volt a korabeli mechanika lehetőségeinek határa. A készülék hanggal jelezte, ha a gép a 7. helyi értékre próbál lépni. Schickard gépe jelezte a számolási tartomány túllépését (a túlcsordulást, overflow).
A szerkezet létezéséről annak idején nem szerezhetett tudomást a világ – Schickard és családja egy pestisjárvány áldozata lett. Érdemes azon elgondolkodni, hogyan befolyásolta volna Pascalt és Leibnizet, ha Schickard gépe megépül és fennmarad.
1642 – Blaise Pascal (1623-1662)
|
|
20 éves korában tervezett és épített egy egyszerű és kicsi gépet, egy hathelyiértékes fogaskerekes összeadó-kivonó gépet, amelyet 1647-ben szabadalmaztatott. Egy Pascal által 1652-ben készített és kézjegyével ellátott gép Párizsban ma is látható a Conservatoire des Arts et Métiers-ben. A gépet Diderot is leírja híres Enciklopédiájában. |
Az egyes számjegyek 0-tól 9-ig fogaskerekek meghatározott beállításának felelnek meg. A számok ábrázolásához annyi, azonos tengelyen elhelyezett fogaskerékre van szükség, ahány számjegyből áll a szám. Az egy fogaskerékfoggal történő elfordítás a forgásiránytól függően 1 hozzáadását vagy levonását jelenti. A 9-ről a rákövetkező 0-ra való átmenet során a gép a legközelebbi helyi értéken álló számot automatikusan eggyel megnöveli, ez az eljárás az átvitel.
Pascal állítólag azért építette meg a gépét, hogy segítségére legyen apjának. Étienne Pascal magas rangú tisztviselő volt Basse-Normandie tartományban, és egy, az adók miatt kirobbant lázadás után újjászervezte a tartomány adózási rendszerét.
1673 – Gottfried Wilhelm von Leibniz (1646-1716)
 |
Minden idők egyik legnagyobb polihisztorai közé tartozott. Szerkesztett egy eszközt, amelyet egyes gépekben még ma is használnak, ez a Leibniz-kerék (bordás henger). Olyan gépet épített, amellyel automatikusan lehetett összeadni, kivonni, szorozni és osztani. Elsőként sikerült két szám szorzását, illetve osztását közvetlenül, egyetlen körülforgatással megoldania. Négy alapműveletes számológépe nyolcjegyű számokkal végzett műveletekhez készült. Saját gépét Pascaléval összehasonlítva kijelentette: ” Mindenekelőtt azt kell megérteni, hogy a gép két részből áll. Az egyiket az összeadás (kivonás) elvégzésére szerkesztették, a másikat a szorzás (osztás) elvégzésére, és a kettőnek össze kell kapcsolódnia. Az összeadó-(kivonó-) gép teljes mértékben megegyezik Pascaléval.” |
1666-ban cikket írt a kombinatorikáról (De Arte Combinatorica). A kombinatorikát úgy írja le, mint “általános módszert, amellyel minden józan ésszel belátható igazság egyfajta számítássá egyszerűsíthető.” Végül érdemes kiemelni négy nagy teljesítményét, amellyel a számolás, a számítás fejlődéséhez hozzájárult:
- kezdeti lépések a formális logika területén,
- ő javasolta először a kettes számrendszer használatát,
- a számolás nem emberhez méltó munka, szükséges és lehetséges automatizálni,
- felismerte, hogy a számológépet hipotézisek ellenőrzésére is fel lehet használni.
Az automata, programvezérelt számítógép gondolata az 1800-as években vetődött fel. A programozott vezérlést egészen más területen használták fel először:
1679 – Kempelen Farkas billentyűvezérlésű hangszintetizátort, “beszélő gépet” épített.
1801 – A francia Joseph Jacquard lyukkártya vezérlésű szövőgépe óriási sikert aratott a párizsi világkiállításon. A lyukkártya biztosította a szövési program (minta) tárolását és a szövőgép vezérlését. Forradalmasította a francia szövőipart.
Charles Babbage (1791-1871)
Leibniz programját – az unalmas, de egyszerű feladatok automatizálásával felszabadítani az embert a rabszolgamunka alól – elsőként a modern intellektuális történelem egyik legkülönösebb alakja, Babbage vallotta magáénak. Babbage-ről helyesen írja életrajzírója, hogy vele kapcsolatban minden vitatott, még születésének időpontja is. Szerinte 1791. december 26-án született Devonshire-ban, ámbár maga Babbage azt állította, hogy 1792-ben és Londonban. Az életrajz címe Irascible Genius (A lobbanékony géniusz), szintén kulcs Babbage-hez.
Egyike a Royal Astronomical Society (Királyi Csillagászati Társaság) alapító tagjainak (1820. január 12.), és őt tüntették ki elsőként a Társaság aranyérmével az Observations on the Application of Machinery to the Computation of Mathematical Tables (Gépek matematikai táblázatok kiszámításánál való alkalmazásának tapasztalatai) c. munkájáért.
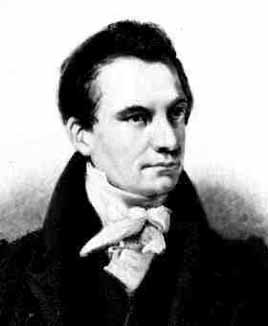 |
Matematikus volt. Bár gépei tisztán mechanikus berendezések voltak, de elgondolásaiban már tartalmaztak sok olyan alapvető lehetőséget, amelyek a modern számítógépekre jellemzőek.
Első gépe (Difference Engine – differenciagép) fix programú célszámítógép volt, mely matematikai táblázatok készítésére volt alkalmas. Ha a táblázatot különféle matematikai műveletek eredményeiből állítják össze, a tapasztalat azt mutatja, hogy a számítást végző ember igen sok hibát vét. A könnyen tévedő embert “csalhatatlan” géppel helyettesíteni – kétségkívül ez volt az az ötlet, amely Babbage-re oly nagy hatással volt.
|
A táblázatkészítés illusztrálása: nézzük az N2+N+41 kifejezés értékét az egymás után következő N=0,1,2,3…9 természetes számok esetére!
N N2+N+41 D1 D2
- 41
- 43 2
- 47 4 2
- 53 6 2
- 61 8 2
- 71 10 2
- 83 12 2
- 97 14 2
- 113 16 2
- 131 18 2
A D1 oszlopot megvizsgálva látható, hogy az N2+N+41 kifejezés egymás után következő elemeinek különbségét tartalmazza; a D2 oszlop – hasonlóan – a D1 oszlop egymás utáni elemeinek különbségéből áll. N=10 esetén az N2+N+41 kifejezés értékét kiszámíthatjuk anélkül, hogy egyetlen szorzást is el kellene végezni. A D2 oszlopba kerülő elem ismét 2 lesz, a D1 oszlopba 18+2=20 kerül, az N2+N+41 jelzésű oszlop következő eleme 131+20=151.
Általában: akárhányad fokú polinomnak van olyan differencia oszlopa, amely már konstans, és így a polinom felépíthető összeadások egymásutánjával. Harmadfokú polinom esetén a D3 oszlop lesz konstans, negyedfokúnál a D4..
Babbage differenciagépe hatodfokú polinomok kezelésére készült. A gép tehát D1, D2, D3..D6 oszlopokkal dolgozott.
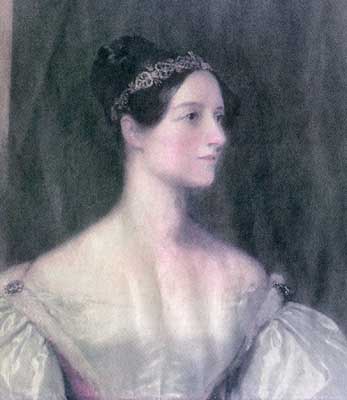 |
Lady Lovelace (Ada Byron) a következőképpen ír: “A gép ennélfogva pontosan és korlátlan terjedelemben táblázatba tudta foglalni azokat a sorozatokat, amelyeknek általános alakja a fenti formába foglalható; és közelítőleg szűkebb vagy tágabb határok között minden más sorozatot is, amelynek kezelésére a differenciák módszere alkalmas.”bb brilliáns kísérletnek kell tekintenünk – ami egy speciális eljárás automatizálására készült – mint a numerikus matematika automatizálására irányuló próbálkozásnak. |
A differenciagép költségeit 1834-ben 17470 font sterlingre becsülték. Összehasonlításképpen: egy mozdony 1000 fontba került. (A londoni Science Museum 1991-ben az eredeti tervek alapján – és a korabeli mechanikai lehetőségek figyelembevételével – rekonstruálta a differenciagép egyik egyszerűsített változatát, amelyet maga Babbage tervezett. Méretei: 3,4m x 0,5m x 2,1m, súlya 3 tonna és 4000 egyedi részből áll. A gép néhány nappal Babbage 200. születésnapja előtt hibátlanul kiszámította a 7. hatványok táblázatának első száz értékét.
1833-ban felhagyott a differenciagép fejlesztésével, kigondolta fő művét az analitikus gépet (Analytical Engine). Ez elvileg egy általános célú számítógép volt, majdnem a modern értelemben. (Szellemében nagyon közel állt a Mark I. nevű Harvard IBM géphez)
Ez a gép életcéljává vált Babbage-nek, és egészen 1871-ben bekövetkezett haláláig dolgozott rajta; halála után pedig fia, H. P. Babbage folytatta a munkát: maga építette meg a gép egyes darabjait, és a londoni Természettudományi Múzeumnak ajándékozta őket.
E gép alapötlete merőben különbözött a korábbi differenciagépétől. Ekkor már meglehetősen világosan látott több olyan elvet, amely a modern számítógépeket jellemzi. Az ötletet a szövőszéken alkalmazott Jacquard-féle szálfűzés megfigyeléseiből merítette. Jacquard kigondolta a szövőszéken a szálak fűzésének egy olyan módját, amely a szövet szövésének folyamatát lényegében automatizálta. Ahhoz, hogy a szövőszéken mintás szövetet szőjön, a szövőnek rendelkeznie kell egy tervvel vagy programmal, amely arról tájékoztatja őt, hogy a nyüst mely szálait kell felemelnie és melyeket leengednie ahhoz, hogy létrehozza a mintát; valamint azt is tudnia kell, hogy mikor kell az alapmintát egyszer használni, vagy többször megismételni.
Jacquard módszerének kulcsa egy kártyasorozat alkalmazása, amelyen lyukak vannak elhelyezve, mégpedig úgy, hogy azok a kívánt mintát rajzolják ki.
Az analitikus gép két részből állt:
- Tároló – mai szóhasználattal memória -, ahol azok a számok helyezkednek el, amelyekkel műveleteket kell végezni. De ide kerülnek azok a mennyiségek is, tehát a részeredmények, amelyek valamely művelet során keletkeztek.
- Malom – angolul: mill -, melybe mindig azokat a számértékeket viszik be, amelyekkel éppen valamilyen műveletet kell végezni. Ez a mai aritmetikai egységnek felel meg.
A gép működéséhez kétféle kártyacsomagra volt szükség. Az egyik a végrehajtandó műveleteket határozta meg (ezek a műveleti kártyák), a másik pedig azokat a speciális változókat tartalmazta (ezek a változókártyák), amelyeken az előbbi csomagnak a műveleteket kell végrehajtani. Babbage felismerte, hogy a részeredmények tárolására szükség van egy belső tárolóra, valamint, hogy a számítási feladatot elemi lépésekre bontva ezen belső tárolók felhasználásával egy külön számolóműben (malomban) kell elvégezni.
A gép, ha elkészül. 1000 db szám tárolását biztosította volna, másodpercenként egy összeadást, percenként egy szorzást végzett volna 50 jegyű számokkal. Az adatok bevitelét és a vezérlést lyukkártya biztosította.
Az analitikus gép rendkívül általános jellegű. Bármilyen formula értékét kívánjuk kiszámíttatni, e számítás szabályait két kártyacsomag útján kell közölnünk vele. Ha ezeket belehelyeztük, a gépet beállítottuk erre a speciális formulára. Ha egyszer a kártyacsomagokat egy adott formulához összeállítottuk, azokat bármely későbbi időpontban ismét felhasználhatjuk, hogy a formula értékét más, esetleg szükségessé váló konstansokkal számítsuk ki újra.
Az analitikus gépnek így saját könyvtára lesz. Bármely, egyszer már összeállított kártyacsomag bármely későbbi időpontban meg fogja ismételni azokat a számításokat, amelyekre eredetileg létrehozták. Ekkor csak a konstansok numerikus értékét kell beadni.
Mindez igen modernnek tűnik. Az analitikus gép titka a kártyacsomagok bevezetése, amelyek hatására a gép automatikusan és az előírt sorrendben hajtja végre a műveleteket.
A gép építése már kezdetben megakadt. A 19. század finommechanikai lehetőségeivel ezt a “programvezérlésű” számológépet nem lehetett megvalósítani. Lady Lovelace (Ada Byron) szerint: “Nagyon találóan mondhatjuk, hogy az analitikus gép algebrai mintákat sző éppúgy, ahogy a Jacquard-szövőgép virágokat és leveleket. Számunkra úgy tűnik, ez a gép messze több eredetiséget mutathat fel, mint amennyire a differenciagép valaha is igényt tarthat.
Babbage munkásságáról a legjobb összefoglalót Augusta Ada Byron írta. (A költő, Lord Byron leánya. Már 15 éves korában kitűnt rendkívüli matematikai képességével. Tiszteletére napjainkban róla nevezték el a nagyszámítógépekre – a Pentagon megbízásából – kifejlesztett ADA programnyelvet.)
1855 – Georg Scheutz (1785-1873)
Svéd nyomdász Babbage gondolataitól indíttatva megépítette a differenciagépet és 1854-ben Londonban – Babbage jelentős segítségével – be is mutatta. 1834-ben az Edinburgh Review-ban megjelent cikkben olvasott Babbage differenciagépéről. A cikk felkeltette érdeklődését és Edward fiával hozzáfogtak egy lényegesen módosított, tökéletesített változat megépítéséhez. 1834-ben a gép működőképes volt, de ötleteiket nem sikerült elfogadtatniuk. 1851-ben a Svéd Akadémia anyagi támogatást nyújtott Scheutznak egy nagyobb és tökéletesebb gép megépítéséhez. Ezt Scheutz 1853-ban fejezte be. A gép 1855-ben a párizsi kiállításon aranyérmet nyert. Scheutzot 1856-ban lovaggá ütötte a svéd király, és a Svéd Akadémia tagjává választották.
Scheutz először ügyvédi gyakorlatot folytatott. Svéd nyelvre fordította a világirodalom több remekművét, többek között Boccacciót, Walter Scottot, Shakespeare műveit. Kiadott azonban technikai és kereskedelmi lapokat is.
A számítógép megvalósításának elméleti alapjait Georg Boole (1815-1864) teremtette meg a logikai algebra (Boole-algebra) kidolgozásával 1847 és 1854 között.
Georg Boole Lincolnban született alsó középosztálybeli családban. Megtanult latinul és görögül, apja pedig meg tudta tanítani a matematika alapjaira. Tizenhat éves korában munkába állt, segédtanári állást vállalt. Ez idő alatt – egyházi pályára készülve – megtanult franciául, németül és olaszul. Húsz éves korában saját iskolát nyitott, ahol maga tanította a matematikát – valójában felsőbb matematikát. Legnagyobb mértékben a formális logika fejlődéséhez járult hozzá. Elsőként állított fel axiómákat, illetve posztulátumokat a logika számára, oly módon, ahogyan Euklidesz és mások tették a geometriában.
Logikájának alaptétele: bármilyen bonyolult logikai kapcsolat megfelelően választott alapműveletek segítségével kifejezhető.
A legjelentősebb gyakorlati lépést a lyukkártyás adatfeldolgozás megvalósítása jelentette a XIX. század végére. Az USA 1890-es népszámlálásánál Hermann Hollerith lyukkártyás berendezéseit használták adatfeldolgozásra.
 |
Hollerith szülei a történelmi jelentőségű 1848-as esztendő politikai forrongásai következtében hagyták el Németországot. Ő már Buffaloban született. A Columbia egyetem bányászati szakát végezte el. Doktori értekezésében egy saját maga szerkesztette táblázatkészítő rendszert tárgyalt. A Columbián folytatott tanulmányai során jó barátságba került korának jól ismert mérnök-pedagógusával, William P. Trowbridge-dzsel, aki álláshoz segítette az 1880-as népszámlálás lebonyolításakor a Népszámlálási Hivatalnál. |
A Népszámlálási Hivatalban az 1880-as években azzal az igénnyel léptek fel, hogy az ott alkalmazott eljárásnak legalább részbeni automatizálására gépi rendszert kellene kifejleszteni.
Hollerith 1879 októberétől 1883 augusztusáig dolgozott a Népszámlálási Hivatal állományában, majd körülbelül rá egy évre a Szabadalmi Hivatalban kapott állást. Ezt követően a népességi statisztikák táblázatba foglalására alkalmas gépének kifejlesztésén dolgozott, és 1889-ben meg is kapta gépére a szabadalmi oltalmat. Ezt a rendszert használták 1890-ben. A kézi adatfeldolgozás több éves munkájával szemben a gépek néhány hét alatt végezték el a munkát.
Kiépített egy kereskedelmi szervezetet, a Tabulating Machine Companyt. 1911-ben ez a társaság átalakult Computer-Tabulating Recording Companyvé, amelyhez 1914-ben lépett be id. Thomas J. Watson. Ebből a társaságból lett később (1924-ben) Watson mesteri irányításával az International Business Machine Company, az IBM.
ELEKTROMECHANIKUS (RELÉS) GÉPEK
Az első, mai értelemben vett számítógép az amerikai Vannevar Bush 1930-as konstrukciója, melyben először alkalmazott e célra jelfogókat, más néven reléket. Ezzel kezdetét vette a relés számítógépek korszaka, amely az 1946-ban megjelenő elektroncsöves gépek megjelenéséig tartott. A relés gépeket a számítógépek nulladik generációjának is szokás nevezni.
A jelfogó (relé) egy kétállású kapcsoló, amelyet egy vezérlőjel működtet. Működésének lényege, hogy a kapcsoló egyik pozíciójában zárja az áramkörök első részét és nyitja a második részét. Másik pozíciójában ezzel ellentétes hatású. Segítségével számokat lehet tárolni. Jelfogók kombinációjával meg lehet valósítani valamennyi logikai függvényt, azaz számítási és logikai műveletek elvégzésére is alkalmasak.
Leonardo Torres y Quevedo (1852-1936) 1914-ben vezette be a számítógép építésben a lebegőpontos számábrázolást. 1910 és 1920 között egyedi számítási célokra (pl. két komplex szám szorzatának kiszámítására) olyan programvezérlésű mechanikus számológépeket épített, amelyek kimeneti egysége írógép volt.
 |
A két világháború közti időszak legsikeresebb konstruktőre az 1910-es születésű német mérnök Konrad Zuse. (képen) 1935-től kezdte el a programvezérelt számítógép kifejlesztését.
1932-ben építette meg az első mechanikus tárolót tetszőleges adatok, elsősorban lebegőpontos ábrázolású (16 bit mantissza, 7 bit kitevő, 1 bit előjel, tehát 24 bit szóhosszúságú) számok tárolására, és 1934-től kezdve kifejlesztette a programvezérlésű számítógépek alapelveit.
|
1938-ban (otthon, szülei lakásának nappali szobájában) építette Z1 néven az első szabadon programozható számítógépet, amely kettes számrendszerben, lebegőpontos ábrázolású számokkal működött. Adatokat billentyűzet segítségével lehetett betáplálni, az eredményt villanyégők sorozata (fénymátrix) jelezte. A számolómű és a tároló telefonrelékből készült.

A Z2 elektromechanikus, mintegy 200 relét tartalmazó aritmetikai egységet foglalt magába. A vezérlő programot kiselejtezett 35 mm-es filmekre lyuggatta.
Az 1941-es Z3, a világ első működőképes, teljesen automatikus, programvezérlésű digitális számítógépe már teljesen elektronikus elemekből épült fel. Lebegőpontos számábrázolás, 22 bit szóhosszúság, 64 lebegőpontos adat tárolására képes tárolóegység, 1600 mechanikus relé a tárolóban, 400 relé a számolóműben (az elektroncsövek még túl drágák és megbízhatatlanok voltak), 3 s alatti automatikus szorzás, osztás és gyökvonás.
Az 1945-ös Z4 ismét elektromechanikus felépítésű volt. Az aritmetikai egység relével, az 500 számot tároló memória mechanikus alkatrészekkel működött. (32 bit szóhosszúság, 64 fixpontos adat tárolása, 5500 relé) 1950-től 1955-ig Zürichben, majd 1959-ig Basel mellett működött.
Zuse elgondolásai és készülékei Németországon kívül nagyon kevéssé befolyásolták a számítógépek fejlődését, mivel Zuse eleinte otthon építette készülékeit, később pedig titoktartásra kényszerült.
Az eredeti Z1, Z2 és Z3 számítógépek megsemmisültek. A Z1 hasonmását utólag megépítették, Berlinben a Közlekedési és Műszaki Múzeumban található.
Colossus. Nagyon gyors, bináris rendszerben dolgozó automata számítógép, amelynek építését Alan Turing kezdeményezte. Kizárólag kódok megfejtésére használták. Angliában készült 1943-ban. 1500 elektroncsövet tartalmazott, kvarcvezérléssel, 5 kHz-es órajellel dolgozott.
Az Egyesült Államokban 1937-ben két csoport kezdett el dolgozni.
 |
Howard G. Aiken, (képen) a Harvard Egyetem fizikusa irányításával és az IBM együttműködésével (WATSON irányításával) hozták létre a MARK I-IV. számítógépeket a haditengerészet és a légierő számára. |
A másik csoport Stibitz irányításával és tervei szerint a Bell Telephone Laboratories keretében a MODEL I-IV. berendezéseket hozta létre. Az első eredményeket Stibitz érte el. Első gépét 1940-ben alkotta meg.(“részben automatikus számítógép”) Ezt követte a “Relay Interpolator”, jelfogós interpolátor. Ez két fő részből állt: 500 telefonreléből és egy távíró-berendezéshez hasonló szerkezetből. Ez számok be- és kivitelére szolgált. A következő a “Ballistic Computer” (ballisztikus számítógép), amely már 1300 relét tartalmazott. Stibitz valamennyi gépe speciális célokra készült, különleges számítások elvégzésére tervezték őket.
MARK I. ASSC (Automatic Sequence Controlled Calculator – automatikusan sorosan vezérelt számítógép). A gép hossza 15,5 m, szélessége 2,4 m volt, tömege 35 tonna. Kb. 400 000 dollárba került. 760 ezer elemet, 800 km-nél hosszabb vezetéket tartalmazott. Percenként 200 műveletet tudott elvégezni. Két szám összeadásához 1/3 másodpercre, összeszorzásához 6 másodpercre, osztáshoz mintegy 12 másodpercre volt szüksége. A számok tárolására 72 db számlálót tartalmazott, ezek mindegyike 23 számjegyet és egy előjelet tudott tárolni. 60 regiszter volt benne az állandók tárolására. Ezeket kézi vezérlésű kapcsolókkal lehetett beállítani. A gépet papírszalag segítségével lehetett vezérelni, amelyre sorosan vitték fel az utasításokat. Mindegyik utasítás három részből állt:
- hol található az az adat, amelyen a műveletet el kell végezni,
- hol kell az eredményt tárolni,
- milyen műveletet kell végezni.
MARK II Jelfogókkal működő elektromechanikus berendezés volt, tízjegyű számokkal tudott dolgozni, ezekből mintegy 100-at tudott tárolni. A MARK I-hez képest mérete ennek háromszorosára, sebessége pedig 12-szeresére nőtt.
MARK III Decimális berendezés volt, 16 jegyű számokkal dolgozott. Szorzási sebessége 80 művelet/perc volt. Ennél a gépnél használtak először mágnesszalagos tárat.
MARK IV. A légierő számára tervezte Aiken, 1952-ben fejezte be.
 |
John Atanasoff (képen) és Clifford Berry 1939-ben 25 bit, később pedig 50 bit szóhosszúságú adatokkal dolgozó bináris összeadógépet építettek. A számítógép lineáris egyenletrendszereket oldott meg. A gép 300 elektroncsövet tartalmazott. A gép további fejlesztésének 1942-ben a háború vetett véget. |
Az ő nyomdokaikon haladva 1942-1946 között a Pennsylvania Egyetemen Eckert és Mauchly, valamint Goldstine irányításával megépült a világon az első modern értelemben vett, kizárólag elektronikus gépe, az ENIAC. (Electronic Numerical Integrator And Calculator = elektronikus és digitális integrator és számítógép)
Az első változat többek között 18000 elektroncsövet, 10000 kondenzátort, 70000 ellenállást tartalmazott. Tömege több mint 30 tonna volt. A gép mintegy 70 m2 területet foglalt el, hossza 30 m, magassága 3 m volt. Az összeadásokat 0,8 ; a szorzásokat 2,8 másodperc alatt végezte el. Működéséhez 120-150 kW teljesítményt igényelt. Viszont sebessége jelentősen megnőtt: kb. 2000-szeres művelet-sebesség növekedést jelentett a legjobb jelfogós gépekkel szemben. Az ENIAC-ot 1947-ben átalakították a Neumann-elvek szerint, így működött 1955-ig.
Az ENIAC néhány hátránya:
- Bonyolult volt a programvezérlés: az önálló egységek külön-külön vezérléssel rendelkeztek, minden utasítás be volt huzalozva, nem volt központi vezérlőegység..
- Nagyon sok elektroncsövet tartalmazott. Az elektroncsövek ezrei keltette nagy hőmennyiséget csak légkondicionálással lehetett ellensúlyozni. A sok elektroncső alkalmazása nagy fogyasztást, gyakori meghibásodást, magas javítási költséget hozott magával.
- Mindössze húsz számot lehetett benne tárolni.
Jelentősége:
- digitális, tehát univerzális gép volt
- elektronikus elven alapult
- bizonyította, hogy az elektronikus elven készült gépek is megbízhatóak.

Az ENIAC (képen) tehát digitális, ezen belül decimális, azaz tízes számrendszerben dolgozott. Hasonlítsuk össze röviden, a teljesség igénye nélkül a digitális és az analóg eszközöket.
Egy analóg számítóeszköz a számokat fizikai mennyiségekként jeleníti meg. Példa erre egy közönséges vonalzó (vagy a logarléc). Bonyolultabb esetben valamely elvégzendő művelet érdekében olyan fizikai készüléket alakítunk ki, amelynek működési szabályai hasonlóak az elvégzendőkkel. (analóg=hasonlóságon alapuló) A problémát (az elvégzendő műveletet) a megépített eszközben szerepet játszó folytonos fizikai mennyiségek mérésével oldjuk meg. (A folytonosan változtatható fizikai mennyiségekkel dolgozó analóg számítógépek működésének alapjait 1876-ban Lord Kelvin dolgozta ki.)
A digitális számítógépek más elven működnek: a számokat számjegyeknek tekinthető diszkrét jelekkel ábrázolják és a négy alapművelet (összeadás, kivonás, szorzás, osztás), valamint logikai műveletek sorozatával oldják meg. (pl. abakusz)
A digitális gépek három szempontból múlják felül az analóg gépeket:
- általánosság:
az analóg eszközök általánossága korlátozott, ugyanis csak egy feladat vagy feladatcsoport megoldására alkalmasak. Egy-egy berendezés képtelen többcélú számítások elvégzésére, ezért tudományos számítások elvégzésére alkalmatlan. Egy digitális eszköz univerzális, azaz segítségével bármely számítási feladat megoldható.
- pontosság:
Az analóg gép pontossága korlátozott, mértékét mindig behatárolja a felhasznált alkatrészek megmunkálásának, illetve azok összeállításának pontossága. A digitális technikában elvben a számolás pontosságának nincs határa.
- gyorsaság:
A digitális technika önmagában nem jelent nagyobb gyorsaságot, a mechanikus és elektromechanikus technológiák korában az analóg eszközök gyorsabbak voltak, mint a digitálisak. Viszont az elektronikus úton megvalósított digitális eszköz gyorsabb, mint egy analóg gép.
Az ENIAC építési munkáinak vége felé csatlakozott a fejlesztő csoporthoz NEUMANN JÁNOS (1903-1957). Mindez véletlenül történt, Goldstine egy vasútállomáson találkozott Neumann Jánossal. Neumann érdeklődését felkeltette ez a munka.

A következő gép az EDVAC (Elektronic Discrete Variable Automatic Computer = elektronikus, diszkrét változós automatikus számítógép) (képen) logikai tervezésében döntő szerepet vállalt. A gépet a Pennsylvania Egyetem Moore Intézetében építették.
Sokan járultak hozzá a mai, modern számítógépek létrejöttéhez, de a magyar Neumann Jánosnak vannak talán a legdöntőbb érdemei.
Megalkotta a számítógép elvi felépítését, logikai rendszerét, alapvető működési modelljét. (Neumann-elvű számítógépek). Az elektronikus számítógépek minőségileg új fokozatot jelentettek, tisztázni kellett, hogy logikai szempontból hogyan működik egy ilyen számítógép. Az elektronikus gépek esetében az adatok, illetve az utasítások tárolását ugyanazzal a sebességgel kell kezelni. Neumann előtt a probléma műszaki vonatkozásaira összpontosítottak. Neumann látta meg először, hogy egy számítógép logikai funkciókat lát el.
Neumann 1945 júniusában kiadott egy, ma már klasszikusnak számító tanulmányt, a “First Draft of a Report on the EDVAC” (Az EDVAC-ról szóló jelentés első vázlata) Itt tárgyalta először logikailag úgy a számítógépet, mintha az csak a matematika vagy logika egyik hagyományos ága lenne. Javasolta a belső programvezérlés megvalósítását a számítógépeknél, hogy az adatok mellett az utasítások is a címezhető belső tárban helyezkedjenek el. Nemcsak az adatokat, hanem az utasításokat is meg lehet változtatni, műveleteket lehet velük végezni, így a számítógép működése sokkal gyorsabb, mint a külső programvezérlésű gépeké.
Ejtsünk néhány szót Neumann János életéről.
Neumann János (John von Neumann)
Neumann János jómódú családban született Budapesten, 1903. december 28-án. Apja, Miksa bankár volt, aki gyermekei számára a szellemi és anyagi jólétet egyaránt biztosítani tudta. Édesanyja Kann Margit. Két öccse született: Mihály (1907), chicagói orvos és Miklós (1911), philadelphiai jogász.
Goldstine írta róla: “Neumann már egészen fiatalon rendkívüli szellemi képességekről és nyelvérzékről tett tanúbizonyságot. Említette egyszer nekem, hogy hatéves korában ő és édesapja gyakran tréfálkoztak egymással ógörögül. Kedvtelésből történelmi tanulmányokat is folytatott.. Később főként a bizánci kultúra történetével foglalkozott, és valóban elmélyült és enciklopédikus tudásra tett szert erről a kérdésről..
Kiváló humorérzéke volt, élvezte az emberek társaságát.
Egyik legfigyelemreméltóbb képessége abszolút emlékezőtehetsége volt. Amennyire csak ellenőrizni tudtam, Neumann képes volt bármilyen, egyszer olvasott könyvet vagy cikket szó szerint idézni; sőt ezt évekkel később is pillanatnyi habozás nélkül meg tudta tenni..
 |
A budapesti Evangélikus Gimnázium tanulója volt, 1921-ben érettségizett. Tanára volt Rátz László, aki rávette édesapját, hogy a kötelező iskoláztatáson kívül magánúton is taníttassa gyermekét. Még 18 éves kora előtt közös dolgozatot publikált tanárával, Fekete Mihállyal. (Rátz László nagy befolyást gyakorolt nemcsak Neumannra, hanem Wigner Jenőre is. Később ő lett az iskola igazgatója.) 1921-ben beiratkozott a Budapesti Tudományegyetemre, de az 1921-23. éveket Berlinben töltötte, innen Zürichbe ment a svájci Szövetségi Műszaki Főiskolára (Eidgenössische Technische Hochschule), ahol találkozott Hermann Weyl matematikussal, aki később kollégája lett a Felsőfokú Tanulmányok Intézetében, és Pólya Györggyel, a legnagyobb matematikaoktatók egyikével. |
A Szövetségi Főiskolán 1925-ben vegyészmérnöki oklevelet szerzett; a következő évben pedig 1926. március 12-én – 22 éves korában – a Budapesti Tudományegyetemen summa cum laude doktorált matematikából. Melléktárgyai a kísérleti fizika és a kémia voltak.
1927-ben a Berlini Egyetem matematika tanszékén egyetemi magántanár lett. Három évig oktatott Berlinben, ezalatt algebrai, halmazelméleti és kvantummechanikai tárgyú dolgozatai révén világszerte ismertté vált. Az 1929-es évet Hamburgban töltötte, 1930-ra meghívták a Princeton Egyetemre vendégelőadónak. Vendégprofesszorként Princetonban maradt, majd 1931-ben az egyetem professzora lett. 1933-ban átment a Felsőfokú Tanulmányok Intézetébe.
1930-ban Neumann házasságot kötött Kövesi Mariettával és 1935-ben megszületett Marina lányuk (aki a Pittsburghi Egyetem közgazdaságtan professzora lett). Neumann házassága 1937-ben felbomlott, 1938-ban feleségül vette Dán Klárát, aki később a Los Alamos-i Tudományos Laboratórium programozója lett, és közreműködött az 1950-es években vizsgált néhány igen nehéz probléma programozásában és kódolásában.
Élénk érdeklődést tanúsított olyan eredmény iránt, amely a modern számítógépek elmélete előfutárának tekinthető. Emil L. Post és Alan Turing 1936-ban egymástól függetlenül közzétett dolgozataikról van szó. Post a New York-i Városi Egyetemen (City College of New York) tanított, míg Turing a Princeton Egyetemen tanuló (1936-1938) angol volt. Mindketten egy ma automatának nevezett matematikai fogalmat tanulmányoztak. A két tudós egymástól függetlenül és egymás tevékenységéről mit sem tudva dolgozott. Kétségtelen, hogy Neumann ismerte Turing eredményét, Postét azonban valószínűleg nem.
Az idő múltával a matematika alkalmazásai iránti érdeklődése egyre nagyobb hangsúlyt kapott, hogy 1941-re érdeklődésének homlokterébe kerüljön. (Érdemes figyelmet szentelni annak a dolgozatának, amit 1928-ban írt a játékelméletről. Ez volt az első próbálkozása ezen a területen, jóllehet mások is tettek e téren kísérleti lépéseket – többek között Borel, Steinhaus és Zermelo -, ő volt az első, aki rámutatott a játékok és a közgazdasági folyamatok közötti kapcsolatra és bebizonyította azóta híressé vált minimaxtételét, amely játékok bizonyos fontos osztályai esetére nyerő stratégia létezését garantálja. Neumann és Morgenstern ismert könyvében a következő olvasható: “megfontolásaink a ‘stratégiai játékok’ elméletének alkalmazásához fognak vezetni, amely matematikai elméletet több egymást követő lépésben dolgozta ki egyikünk 1928, majd 1940-41 folyamán.”)
Az 1930-as évek közepére Neumann mélyen elmerült a folyadékok és gázok hangsebességnél gyorsabb, turbulens áramlásának problémájába. “Ekkortájt ismerte fel a nemlineáris parciális differenciálegyenletek témakörének alapvető titkait.. E nemlineáris egyenletek által leírt jelenségek analitikusan teljesen követhetetlenek, és még a jelenleg ismert kvalitatív vizsgálati módszerekkel is megközelíthetetlenek.”(Ulam) Így a II. világháború elejére Neumann a lökés és robbanási hullámok vezető szakértőinek egyike lett és szükségképpen került kapcsolatba a Ballisztikai Kutató Laboratóriummal, az OSDR-vel, a Hadianyag-ellátási Főnökséggel és a Manhattan-tervvel.
Neumann érdeklődött a numerikus számítások iránt és hatalmas tehetsége volt hozzá. Hidrodinamikai munkássága azonban számítógépek és a gépi számítás nélkül nem lehetett volna eredményes. Az a véletlen műve, hogy az ő személyén keresztül létesült kapcsolat Aberdeen és Los Alamos között. Ennek a véletlennek azonban valamennyien sokat köszönhetünk.
Goldstine írja: “Valamikor 1944 nyarán, miután elhagytam a kórházat, az aberdeeni vasútállomás peronján vártam a Philadelphiába induló vonatot, amikor egyszer csak arra jött Neumann. Ezt megelőzően sohasem találkoztam a nagy matematikussal, bár természetesen sokat tudtam róla, és több alkalommal hallgattam előadását is. Meglehetős vakmerőség volt tehát részemről, hogy odamentem ehhez a világhírű emberhez, bemutatkoztam és beszélgetni kezdtem. Szerencsémre Neumann barátságos ember volt, aki mindent megtett annak érdekében, hogy az emberek ne érezzék magukat feszélyezve jelenlétében. A beszélgetés során hamar szó esett munkámról. Amikor Neumann megértette, hogy egy olyan elektronikus számítógép kifejlesztésén dolgozom, amely másodpercenként 333 szorzás elvégzésére képes, beszélgetésünk humoros, kötetlen légköre egyszeriben megváltozott, és sokkal inkább a matematikai doktori fokozat elnyeréséhez tett szóbeli vizsgám légköréhez kezdett hasonlítani.
Nem sokkal ezután mindketten Philadelphiába mentünk, ahol Neumann megtekintette az ENIAC-ot… Még ma sem tudom derültség nélkül felidézni Eckertnek a küszöbön álló látogatással kapcsolatos reakcióját. Azt mondta, hogy amint Neumann az első kérdését felteszi, ő meg tudja mondani, valóban zseni-e vagy sem. Ha a kérdés a gép logikai struktúrájára fog vonatkozni, ő is hinni fog Neumannban, egyébként nem. Neumann első kérdése természetesen ez irányú volt.
1944. november 2-án feleségemmel együtt visszatértünk Philadelphiába, és ismét ott telepedtünk le. Ekkor kezdődött hosszú és rendkívül gyümölcsöző baráti és munkakapcsolatunk Neumann-nal, amelynek csak az ő korai halála vetett véget.”
1933-tól 1957-ig Princetonban a Felsőfokú Tanulmányok Intézetének Matematikaprofesszora volt.
Washingtonban halt meg 1957. február 8-án.
Neumann logikailag teljes elemzését adta az EDVAC szerkezetének. “First Draft”-ja a gépek egész sora leírásának alapjává vált. Egy ilyen gép öt fő egységből áll: az aritmetikai egység, amely az elemi aritmetikai műveletek végrehajtására képes; a központi vezérlőegység, amely a kapott utasításokat hajtja végre; a memória tárolja az adott problémához szükséges numerikus adatokat és az utasításokat, végül az input és output (beviteli és kiviteli) egységek biztosítják az ember és a gép közötti kapcsolatot.
Neumann fogalmazta meg a számítógépek működésének öt fő alapelvét:
-
Teljesen elektronikus számítógép. A gép egyszerre csak egy műveletet végez, de mindezt igen gyorsan.
-
Kettes számrendszer használata. A tízes számrendszer megfelelt a mechanikus szerkezeteknél, a kettes számrendszert elektronikusan sokkal könnyebb megvalósítani a kétállapotú jelekkel.
-
Belső memória alkalmazása. A számítógép gyors működésébe nincs értelme emberi erővel beavatkozni, Neumann javaslata szerint a gépbe kell egy belső memória, amelyben a részeredmények tárolhatóak, s így a gép egy bizonyos műveletsort automatikusan is el tud végezni.
-
Tárolt program elve. A számítások menetére vonatkozó utasítások kifejezhetőek számmal, azaz adatként kezelhetőek. Ezeket éppúgy tárolhatjuk a belső memóriában, mint az adatokat.
-
Univerzális számítógép. Különböző feladatok elvégzésére nem kell speciális gépeket építeni. (A 30-as években Turing angol matematikus a matematikai logika eszközeivel kimutatta, hogy az olyan gép, amely el tud végezni néhány alapvető műveletet, elvileg bármilyen számítás végrehajtására alkalmas.)
A számítógép részei:
-
Aritmetikai-logikai egység: a központi feldolgozó egység egyik alegysége. Aritmetikai és logikai műveleteket végez, kiértékeli a relációkat.
-
Vezérlőegység: dekódolja, értelmezi a program soron következő utasítását, ennek megfelelően vezérli a többi egység működését.
-
Belső memória: vagy operatív tár – itt vannak azok az adatok és utasítások, amelyek a futó program működéséhez szükségesek. Meg kell említeni a háttértárolókat is, mert a gyors működésű operatív tár viszonylag kevés adat tárolására alkalmas. Ezek mágneses elven működő berendezések (lemezegységek, mágnesszalagok, streamerek) igen nagy mennyiségű adat tárolására alkalmasak. (A mágneses jelrögzítés fizikai elve az elektromágneses indukció.) A programok az adatokhoz hasonlóan szintén tárolhatók a háttértárolókon.
-
Be/kiviteli eszközök: a számítógép és a felhasználó közötti kapcsolatot valósítják meg. (Az információáramlás irányától függően beszélünk beviteli, kiviteli vagy be/kiviteli eszközökről.)
Neumann munkatársa volt az angol Wilkes, aki 1946 és 1949 között megépítette Angliában, Cambridge-ben az EDSAC-ot. (Electronic Delay Storage Automatic Calculator – késleltetett tárolású elektronikus automatikus számológép). Ez a gép – Wilkes hangsúlyozta is – Neumann elvei alapján épült fel.
1946-ban Eckert és Mauchley megvált a Moore Intézettől, közös társaságot alapítottak és megépítették a BINAC-ot. (Binary Automatic Computer – univerzális számítógép).
1950-ben helyezték üzembe. 1947-től kezdték el építeni az UNIVAC-ot. (Universal Automatic Computer – univerzális automatikus számítógép). A gép továbbfejlesztett változata került először nagykereskedelmi forgalomba.
 |
Princetonban készült Neumann és Goldstine vezetésével az IAS gép. (Az intézet neve után “hívták” így a gépet. Institute for Advanced Study) Ebben a gépben (képen) már “párhuzamos” aritmetikai egység működött. ( az összeadás során az egyes számjegyek párjait egyidejűleg adták össze)
|
Nagy jelentőségű volt a folyamatábra kialakítása is. Neumann és Goldstine a programozás kapcsán dolgozta ki ezt az ábrázolásmódot, amely egyben kitűnő tervezőeszköz is. (A folyamatábra szabványban meghatározott szimbólumok rendezett sorozata, amelyben az egyes elemek a probléma meghatározásának, elemzésének vagy megoldásának a résztevékenységeit – lépéseit – jelentik.)
Az IAS gép programozásával kapcsolatban vezették be az un. vezérlésátadó utasításokat. Ekkor született meg az indexregiszter fogalma.
A számítógépek további fejlődése szorosan összefügg a felhasznált alkatrészek gyártási technológiájával. A rendelkezésre álló alkatrészbázis, a gyártási technológia meghatározó a számítógép áramköreinek fizikai megvalósításánál. Befolyásolja a számítógép rendszertechnikai felépítését és az alkalmazható programok, eljárások, szabályok fejlettségét is.
Első számítógépgeneráció: 1946-tól 1954-ig terjedő időszak. Hatása azonban az ötvenes évek végéig megmutatkozott. Elektroncsöves, digitális gépek. Kis műveleti sebesség (103 – 104 művelet/sec.), nagy méret, nagy teljesítményfelvétel (10..100 kW), kis megbízhatóság, magas ár. Felépítésük processzorcentrikus volt, minden adatforgalom a központi feldolgozóegységen keresztül zajlott. Csak a soros feldolgozásra volt lehetőség, egy időben csak egyféle művelet folyhatott. Az alkalmazott operatív tárak késleltető művonalat vagy elektroncsöves áramköröket használtak tároló elemként. A perifériák egyedi, gépenként különböző eszközök voltak. A programozás gépi kódban, majd assembley szintű gépi nyelven történt. Főleg tudományos-műszaki számításokra használták őket.
Második számítógépgeneráció: kb. 1954-től 1964-ig tartott. Félvezetős áramköröket tartalmaztak. Megbízhatóságuk, műveleti sebességük nőtt (104 – 105 művelet/sec.), teljesítményfelvételük jelentősen csökkent. Rendszertechnikailag lényeges változást jelentett az önálló, központi feldolgozóegységtől függetlenül, azzal párhuzamosan működő csatornák megjelenése. A számítógép struktúrája memóriacentrikussá vált.
A hagyományos perifériák mellett elterjedtek a nagy tömegű adat és program tárolását és gyors átvitelét biztosító mágneslemezes és mágnesszalagos háttértárak. Az operatív tárak ferritgyűrűs felépítésűek, megbízhatóbbak, gyorsabbak, nagyobb kapacitásúak lettek.
Megjelentek a gépcsaládok, a különböző teljesítményű, de azonos módon programozható, azonos perifériákat használó “kompatíbilis” számítógépek. Megnőtt a software jelentősége, magas szintű programozási nyelvek alakultak ki: FORTRAN, ALGOL, COBOL.
 |
1964-ben Kemény János (képen) és Thomas Kurtz a Dartmouth College-ben kifejlesztették a BASIC nyelvet. Kialakult a folyamatos működést automatikus programváltással biztosító kötegelt (batch) feldolgozási mód, és az ezt megvalósító programok rendszere az operációs rendszer. A számítógépet a gazdasági életben (adatfeldolgozás) és az iparban (folyamatirányítás) is széles körben kezdték alkalmazni.
|
Harmadik generációs számítógépek: 1964-től 1971-ig tartott. Diszkrét félvezető eszközök helyett 10..1000 félvezető elemet egy tokban tartalmazó integrált áramkörökből (integrated circuits) épültek fel. Ez az előző generációhoz képest ismét sebességnövekedést (105 – 106 művelet/sec.), méret- és teljesítményfelvétel csökkenést jelentett.
Rendszertechnikailag jellemző a modularitás, a modulok önálló, párhuzamos működése.
Ez időszakban fejlesztették ki az IBM 360-as számítógépcsaládhoz tartozó DOS és OS operációs rendszereket. 1969-ben indult a UNIX operációs rendszer, 1970-ben a C nyelv fejlesztése a Bell Laboratóriumban.
 |
Nicklaus Wirth, (képen) a Zürichi Műszaki Egyetem professzora 1968-ban készítette el a Pascal nyelv terveit, az első fordítóprogram 1970-ben készült el.
|
Negyedik generációs számítógépek: kb. 1971-től a 90′-es évek közepéig. Jellemzői a mikroprocesszorok és a személyi számítógépek térhódítása, korábban elképzelhetetlen működési sebesség, tárolási sűrűség és kapacitás, illetve miniatürizálódás, nagyfokú integrálás.(LSI Large Scale Integrated, VLSI Very Large Scale Integrated)
Egy tokban 10000..100000 áramköri elemet realizáltak, lehetővé tették a számítógép egy tármoduljának vagy processzorának egy elemként történő megvalósítását.
Új típusú háttértárak jelentek meg (floppy, winchester). A személyi számítógép tömegcikké vált. Az interaktivitás fokozását speciális perifériák segítik (egér, joystick, scanner). A nyomtatók minősége elérte a nyomdai szintet.
Meghatározó jelentőséget kaptak a számítógépes elektronikus hálózatok és a grafikus operációs rendszerek. A korábbinál lényegesen hatékonyabb programozási nyelveket terveztek. Jelentősen bővült a számítógépek addigi felhasználási köre – kiadványszerkesztés, CAD, CASE rendszerek, animáció, táblázat- és adatbáziskezelők, mesterséges intelligencia, szimuláció, szakértői rendszerek.
A negyedik generáció kezdetének a világ első mikroprocesszorának megjelenését tekintjük. Ez az Intel cég 4004-ese, amelyet Ted Hoff mutatott be az Egyesült Államokban 1971-ben. 2250 komponensével 11 millió négybites számpár összeadására tették alkalmassá.
1972: Zilog Z80-as, MOS Technology 6502-es, Motorola 6800-as mikroprocesszorok.
1974-ben készült el a John Backus által tervezett párhuzamos architektúrájú gép, az IBM CLIP-4.
1975: Ed Roberts: az első bemutatott személyi számítógép (Altair 8080) az Intel 8 bites, 8080-as mikroprocesszorára alapozva (saját kezűleg összeszerelhető, billentyűzet és monitor nélküli számítógép, a dobozon lévő kapcsolókkal lehetett adatokat bevinni a 4 Kilobyte memóriába, lámpák felgyulladása jelezte az eredményt, nem tartozott hozzá magas szintű programozási nyelv). Az Altair számítógépre az első magas szintű programozási nyelvet (BASIC-et) Bill Gates és Paul Allen fejleszti ki, ennek köszönhetően alapítják meg a Microsoft céget.
1976: Texas Instruments 16 bites TMS 9000 mikroprocesszor.
1979: Az Intel új mikroprocesszorral jelentkezett, a 8080-assal, melyet 4500 elektronikus komponense két és félmillió nyolcbites szám összeadására tett alkalmassá másodpercenként. /XT-hez.
1980: Sinclair Zx 80-as Z80 CPU, 1 Kb RAM, 4 Kb ROM.
1981: a Xerox Star rendszer, az első Wimp rendszer (windows, icons, menus, poiting device röviditése, a grafikus felhasználói interfész másik neve).
1981: Hewlett-Packard szuperchip (45000 komponens tartalmaz, 1,8 millió, két 32 bites számot tud összeszorozni másodpercenként).
1982: Commodore 64-es (6510 CPU, 8 Kb ROM-ban Basic értelmező)
1982: Intel 80286 mikroprocesszor (AT-hez).
1983: IBM PC/XT Intel 8088 CPU, 10 Mb merevlemezes tároló.
1984: Apple: Macintosh számítógép (grafikus felülettel rendelkezik). Elődjeit az Apple-t és az Apple-2-t Steve Wozniak és Steve Jobs hozták létre.
1984: IBM PC/AT Intel 286-os CPU, RAM 256, belső sínrendszere 16 bites, 1,2 Mb floppy lemezes tároló.
1985: Inmos cég (Egyesült Királyság) T414 transzputer, az első mikroprocesszor beépítése párhuzamos számítógépbe. A hagyományos számítógép áramkörei az adatok feldolgozását egymás után, sorban végzik, míg a transzputer áramkörei párhuzamosan. Transzputerre az OCCAM programozási nyelven írt programmal a számítási sebesség jelentősen csökkenthető.
1986: Intel 80386 mikroprocesszor.
1987: IBM PS/2 termékcsalád, OS/2 operációs rendszer.
1988: Compaq Desk pro AT 368-os.
1989: Wafer-skálájú szilícium memória-chip (söralátét nagyságú, 200 millió karakter tárolására képes). Japán: 4 millió bit tárolására képes memória chip a tömeggyártásban (9 millió komponensből áll és 520000 karakter tárolására képes)
1990: Microsoft: Windows 3.1. ALR 486-os EISA sínrendszerrel.
1992: Sanyo Electric: magas hőmérsékleten szupervezető kerámia tranzisztor (időben tízszer gyorsabb a félvezetős tranzisztornál). Philips, Sony: CD térhódítása.
1993: Personal Digital Assistant: kézírás-felismerő gép. Intel: 64 bites Pentium processzor, amely két különálló program párhuzamos futtatására képes.
Ötödik generációs számítógépek: A multimédia és az Internet világméretű térnyerése, egy-egy új számítógép generáció kezdőévét még utólag sem egyszerű behatárolni. Az átmenetek nem feltétlenül ugrásszerűek.
Valószínűleg általánossá válnak a Tbyte-os háttértárak, a Gbyte-os operatív tárak, a transzputerek, az emberi szem felbontóképességéhez jobban illeszkedő képernyők, az integráltság mértéke növekszik, nagyobb futási sebesség, párhuzamos feldolgozás.
Az optikai számítógép – amelyekben nemcsak elektromos jelek, hanem fény is továbbítja az információt -, előretörése valószínű. Prototípusát a Colorado-i Egyetemen készítették el 1993-ban.
Új típusú adathordozók is megjelenhetnek. A CD továbbfejlesztésével (vagy akár egy új technológiával?) olyan háttértárak nyerhetők, amelyek terjedelmes mozgófilmek tárolására alkalmasak. A számítógép, a tv, a video, a hifi-berendezések, az óriási sebességű háttértárak, professzionális képernyők és a mainál fejlettebb processzorok új típusú számítógépek létrejöttét eredményezi.
A programozott oktatófilmek a tanulásnak egy más eszközét adják talán. A beszéd alapú interaktivitás jellemzővé, általánossá válik. A természetes nyelvek közti fordítóprogramok színvonala olyan mértékben fejlődhet, hogy bármely két nyelv között oda-vissza képesek lesznek a tolmácsolásra. E funkciókat támogatja (majd) az Internet; a számítógépek rádiós, műholdas összeköttetését is lehetővé teszi.
Akármennyi számítógép interaktív kapcsolatot teremthet egymással. A tv, a rádiótelefon és az Internet nyújtotta információszórás egy magasabb rendű szintézisben új dimenziókat nyit meg. Az ötödik generáció tehát az információszórás, -feldolgozás, -tárolás új tartalmat nyerő korszaka lesz. A programkészítésben általánossá válnak a generátor típusú fejlesztőeszközök, amelyek a programozó igényének megfelelően, vele interaktív módon tervezett rendszerek készítését teszik lehetővé.
A hatodik generáció talán a biológiai elvek alapján működő számítógépeké lesz.
NÉHÁNY SZÓ A MAGYAR INFORMATIKÁRÓL
(A 30-as évektől az 60-as évek végéig)
Nemes Tihamér (1895-1960) postamérnök volt, aki a 30-as években kezdett el kibernetikai gépek tervezésével foglalkozni. Posztumusz munkáját (Nemes Tihamér: Kibernetikai gépek. Akadémiai Kiadó. 1962) barátai rendezték sajtó alá. Tanulmányai, találmányai “az emberi cselekvés és gondolkodás megismerését mérnöki módszerekkel, szerkezeti elemekkel, áramkörökkel közelíti meg”.
Kozma László (1902-1983) mérnök, akadémikus. Pályáján telefonműszerészként indult, mérnöki diplomáját Brünnben szerezte. 1930-tól a Bell Telephone antwerpeni gyárában telefonközpont fejlesztőként dolgozott, az azt követő néhány éves tevékenysége a számítástechnika belgiumi történetéhez tartozik. 1938-ban megbízták, hogy tervezzen és építsen a gyárban használatos telefonközpont elemekből automata számológépet. Decimális gépet tervezett, amelynek legfontosabb eleme a 11 ívpontos kapcsológép volt. Ezt a szabadalmat további kilenc követte, amelyek közül a géptávírókkal és mágnes huzalos tárolókkal távfeldolgozási üzemben működő könyvviteli rendszert kell kiemelni.
1955-ben tervezte és építette meg a Budapesti Műszaki Egyetem első és egyetlen jelfogós bináris számítógépét, a MESZ 1-et. A gép programvezérelt, de a szó ismert értelmében nem tárolt programú volt. A berendezés kb. 2000 db (10 féle) jelfogóból épült, az adatokat bebillentyűzték. Az eredmény kiírására egy írógépet alakítottak át, a billentyűket elektromágnesek húzták meg. Fogyasztása kb. 600-800 W volt. A programot egy kézzel lyukasztott lapon tárolták. A gép egycímű utasításokat használt, egy lapra 45 utasítás fért rá, ezenkívül 9 konstans. A jelfogós adattárban 12 db 27 bináris számjegyű számot lehetett tárolni. A gépben automatikus 10 à 2 és 2 à 10 átalakító volt beépítve. A gép építésében részt vett Werner János (Svédország), majd továbbfejlesztésében Frajka Béla docens. A gép kb. 10 évig működött, ma nagyobbik része az Országos Műszaki Múzeum raktárában van elhelyezve, szekrénye a Neumann János Számítógép-tudományi Társaságnál van kiállítva.
Kalmár László (1905-1976) matematikaprofesszor, aki formális logikát is előadott a szegedi József Attila Tudományegyetemen, tervezte meg és munkatársával, Muszka Dániellel együtt építették meg 1958-60-ban az ún. Szegedi- vagy Kalmár-féle logikai gépet. Egy háromvezetékes huzalrendszerrel lehetett programozni, jelfogókból és számjegygépekből összeszerelt vezérlőmű vizsgálta meg a programozott logikai feladat minden egyes variációját, és megállapította, hogy a kívánt bonyolult ítéletsorokból álló összetett ítélet milyen feltételek mellett igaz vagy hamis.
A gép sikeres kísérlet volt, gyakorlati feladatokat is megoldottak vele, de főleg az oktatás céljait szolgálta, az 1960-as Budapesti Nemzetközi Vásáron mutatták be. Kalmár László a halála előtti években egy új, ún. “formulavezérlésű” gépet tervezett, amely az emberi kommunikációhoz közel álló módon lett volna programozható. Terveinek befejezését korai halála akadályozta meg.
Muszka Dániel és Király József még a logikai gép befejezése előtt bemutatták az ún. “Szegedi Katicabogarat, ami a pavlovi feltételes reflexek és egyéb agyi funkciók analógiájára működött.
A Magyar Tudományos Akadémia Kibernetikai Kutató Csoportja 1956-ban a Műszeripari Kutató Intézet egyik osztályaként alakult meg. 1957-ben az osztály a Magyar Tudományos Akadémiához került önálló kutatócsoportként. Igazgatója Varga Sándor lett. A Szovjetunióban akkor frissen tervezett számítógép, az M3 terveit vették át és a tervek alapján építették meg a gépet. Ebben sok logikai, de elektronikai hiba is volt, ezeket részben a ritka szovjetunióbeli konzultációk alkalmával, részben pedig önállóan javították ki, ezért a két, a szovjet és a magyar gép sok megoldásban eltért egymástól. A gép 1959 elejétől működött. A legnagyobb gondot az elektroncsövek okozták. A gép átlagban 1 – 1,5 műszakot üzemelt a hét öt napján, kb. 240-280 órát havonta. A használt szovjet csövek kb. 600 órára voltak méretezve. A másik hibaforrás a mágnesdob volt. A gép bekapcsolásakor a hőtágulás miatt az eredetileg üzemi körülmények között beállított fix író – olvasófejek közelebb kerültek a felülethez, ez azt jelentette, hogy néhány tíz m m vastag mágneses réteget a fejel egyszerűen lenyúzták az alaptestről.
A teljes gépet áttervezték, az alegységekben a csöveket kicserélték hosszú időtartamú (3000 órás) rádiócsövekre, amelyeket az Egyesült Izzó akkor már gyártott. Igen nagy munka volt, mert más paraméterű csövekről volt szó, így az áramköröket is újra kellett méretezni. A mágnesdob vezérlőjét áttervezték, egyben két mágnesdob összekapcsolását is megoldották. A következő fejlesztésként az Intézet ferritgyűrűs tárat vásárolt, így a gép teljesítménye 30 művelet/s-ról 1500 művelet/s-ra növekedett.
A hatvanas évek elején a központ munkatársai a gépet továbbfejlesztették pl. új utasításokat építettek bele, zenélő adapter készült. Elkezdődött a programfejlesztés és a számítógéphez illő alkalmazási feladatok kiválasztása, algoritmizálása és programozása.
Központi Fizikai Kutató Intézet 1959 körül vásárolt a Szovjetunióból egy URAL 1-es számítógépet. A KFKI-ben alapításától fogva jelen volt a fizika mellett a digitális elektronika is. A számítógép fejlesztés – a TPA program – a sokcsatornás analizátorok fejlesztési bázisán indult a 60-as évek közepén. 1960-ban kifejlesztették a 128 csatornás analizátort, amely elektroncsövekkel és itthon gyártott ferritmemóriával készült el 1963-ban. Kb. 50 ilyen berendezés épült. 1965-ben készült el a tranzisztoros változat, amelyet már Tárolt Programú Analizátornak neveztek. Ebből a fejlesztési eredményből már csak egy nagyon kis lépés volt egy általános célú számítógép létrehozása. A KFKI a DEC kompatíbilis utat választotta, így jött létre a TPA-8, ezt követte a TPA-10 és még egy sor új típus.
EMG (Elektronikus Mérőkészülékek Gyára) ők fejlesztették ki a HUNOR digitális, négy alapműveletes, automatikus számológépet, majd a hatvanas évek második felére az EMG 803-as tranzisztorizált általános célú számítógépet.
Telefongyár A korai számítógépek fejlesztésébe az EDLA programmal kapcsolódott be. A rövidítés Dr. Edelényi László és Dr. Ladó László feltalálók nevét takarja.
Az EDLA-I.-et a Telefongyár új elektromos könyvviteli gyűjtőberendezéseként hirdették és mutatták be 1959-ben a Budapesti Nemzetközi Üzemszervezési Kiállításon. Az EDLA-II. teljesen tranzisztoros áramkörökből épült, elektronikus könyvelési adatgyűjtő berendezés bemeneti berendezésekből, adattároló mágneses memóriából, műveletvégző egységből és kimeneti berendezésből állt.
- Az első, fából készült logikai gép: Nemes Tihamér.
- Az első jelfogós és programozható számítógép: Kozma László és munkatársai.
- Az első kibernetikus állatmodell: Muszka Dániel.
- Az első jelfogós logikai gép: Kalmár László és munkatársai.
- Az első digitális, automatikus, tárolt programú számítógép (Neumann-elvű) az M3 volt.
- Az első elektronikus könyvelési rendszer az EDLA-II.
- Az első elektronikus asztali számológép a HUNOR volt.
- Az első sikeres, sorozatban gyártott tranzisztorizált gép a TPA-8.
A hatvanas évek elején a felhasználók többnyire már nem saját maguk fejlesztettek, hanem vásárolták a számítógépeket. Ezeket a gépeket elsősorban a kutatóintézetek vagy egyetemek használták, de néhányat már a termelésben, ill. az üzleti életben is alkalmaztak.
Felhasznált irodalom
H. H. Goldstine: A számítógép Pascaltól Neumannig
Műszaki Könyvkiadó, Budapest,1987.
Csajbók Zoltán: A számítástechnika története
ÉGSZI-Scola Alapítvány, Budapest, 1992.
Zsom Gyula: Digitális technika
Műszaki könyvkiadó, Budapest,1990.
Hans Breuer: SH atlasz – Informatika
Springer Hungarica Kiadó, 1995
Számítástechnikai Lexikon – Az alapok
Kossuth Könyvkiadó, Budapest, 1996.
forrás: http://www.kobakbt.hu

